티스토리 뷰
https://www.youtube.com/watch?v=QpOuyqd6nnc&t=4s
https://www.youtube.com/watch?v=ZI800-2jv38
Graphs and Trees
로봇의 C 공간은 연속적인 공간이지만, 모션 계획에서는 일반적으로 어떤 방식으로든 분리/범주화(discretize) 된다.
미로 속에 모바일 로봇이 있다고 하자.
몇 가지 갈림길에 우리는 점을 찍을 수 있고, 그 경로에서 선을 그려서 로봇이 움직일 수 있는 경로와, 그 여유 공간을 나타낼 수 있다.
그러면 그렇게 이어진 선은 graph로 표현할 수 있다.
이 그래프는 노드들과 간선의 세트로 구성된다.
예를 들어, 그냥 a~e의 노드가 있고, 각각 그냥 선으로만 연결되어 있다고 하자.
비가중 무방향 그래프이다.
각 모서리는 어느 방향으로든 갈 수 있고, 그냥 최단 경로를 택하면 된다.
그러나 만약 가중 방향 그래프라면 간선마다 비중이 다르다.
각 노드에서 노드로 가는 데 있어서 걸리는 에너지나 시간의 양이 다르므로 최적 경로를 찾아야 한다.
또한 양방향 그래프도 존재한다. 유향 그래프는 digraph라고도 한다.
마지막으로 트리를 특정 유형의 유향 그래프로 정의하게 된다.
하나의 뿌리 노드가 있고, 부모 노드에서 자식 노드로 가며, 사이클이 없다.
따라서 우리는 이런 그래프에서 최적의 경로를 찾는 A-star search 알고리즘이 필요하다.
A-star 알고리즘
자유 C 공간을 그래프로 표현하는 것이 일반적이다.
edge는 구성간의 자유 경로를 나타낸다.
그래프가 있으면 그래프를 검색해서 시작 node와 목표 node 사이의 경로를 찾아야 한다.
간선이 구불구불할 수도 있다고 가정한다.
그러면 시작점과 목표 사이의 비용을 최소화해야 한다.
그러므로 간선은 일단 직선으로 간소화하고, 각 cost를 할당한다.
그러면 가중치가 부여된 무방향 그래프가 생긴다.
A-star는 개별 간선이 양수 비용 그래프에서 그 합으로 최저 비용 경로를 찾는데 사용된다.
즉, 경로 비용이 양수여야 한다.
Optimistic cost-to-go
A-star 검색에는 그래프 외에도 Optimistic cost-to-go라는 개념이 있다.
Optimistic cost-to-go : A lower bound on the actual cost to go from a node to a goal node
노드에서 목표 노드로 이동하기 위한 실제 비용의 하한
An estimate of the cost-to-go is optimistic if the actual cost-to-go can never be less the the optimistic estimate
실제 투입 비용이 최적의 추정치보다 결코 작을 수 없는 경우 투입 비용의 추정치는 최적이다.
Optimistic cost-to-go를 계산하는 데는 두 가지 기준이 필요하다.
- 첫번쨰 : 빠르게 평가하기에 적합해야 한다.
- 두번째 : 최적의 추정치가 합리적이도록 실제 투입 비용과 가까워야 한다.
0 cost-to-go로 예측하는 함수는 첫번째 가정을 만족시키지만,
가장 적절한 추정치를 내놓아야 한다는 두 번째 가정을 만족시키지 못한다.
또한 모든 경우를 다 따져서 완벽하게 추정치를 내놓는 함수 또한 첫번째 가정을 만족시키지 못한다.
아주 명확한 예시로는 start에서 goal로 직선으로 가는, 예를 들어 새가 나는 경우를 생각해볼 수 있다.
이것은 아주 빠르게 평가하기에 적합하고, 최적의 추정치를 내놓는다는 합리적인 계산이다.
이를 베이스로 계산해보자
실제 계산
노드 1에서 6까지 가는 목표 있다고 하자.

| 1 | 2 | 3 | 4 | 5 | 6 | |
| past cost | 0 | inf | inf | inf | inf | inf |
| optimist ctg | 20 | 10 | 10 | 10 | 10 | 0 |
| est tot cost | 20 | inf | inf | inf | inf | inf |
| parent node | - | - | - | - | - | - |
1에서 1로 가는 cost는 당연히 0이다
그리고 나머지 노드는 무한인데, path가 있는지 없는지 모르기 때문이다.
그 다음에는 optimist ctg(최적화 거리)에 나머지 노드에서 6까지 가는 직선 거리를 가정해보자.
1은 노드 2개를 거치므로 2*10, 나머지는 10, 6은 0임을
estimated total cost는 past+cost와 optimist ctg를 더해준다.
왜냐하면 1에서 6까지 간다는 예상 거리가 그렇게 나왔기 때문.
parent node는 1에 부모 노드가 없으므로 -, 나머지 노드는 어떻게 되어 있는지 모르므로 저렇게 표시해준다.
이제 리스트 2개를 정의해준다.
OPEN = 탐색할 노드 목록
CLOSED = 이미 탐색한 노드 목록
시작 노드인 1을 사용하여 OPEN 목록을 초기화한다.
OPEN : 1(20)
1->6 예상 총 비용인 20을 표시한다.
이제 OPEN의 첫번째 노드부터 탐색하여 검색을 시작한다.
노드 1에서 멀어지는 모든 간선을 탐색한다.
첫번째는 1->3
현재 노드 3에는 상위 노드가 없으므로, 이를 업데이트하여 노드 1에서 노드 3에 도달할 수 있음을 나타낸다.
또한 노드 3은 18이므로, past cost를 18로 업데이트한다.
그러면 새로운 est total cost는 28이 된다.
이제 노드 3을 OPEN의 목록에 추가하고 예상 비용에 따라 정렬된 순서로 목록에 삽입한다.
OPEN : 1(20), 3(28)
이런 방식으로 1->4, 1->5도 반복

| 3 | 4 | 5 | |
| past cost | 18 | 12 | 30 |
| optimist ctg | 10 | 10 | 10 |
| est total cost | 28 | 22 | 40 |
| parent node | 1 | 1 | 1 |
현재 OPEN : 1(20), 3(28),4(22),5(40)
정렬하면 1(20), 4(22), 3(28),5(40)
노드 1에서 탐색을 마쳤으므로, OPEN의 노드 1을 CLOSED 목록으로 이동한다.
CLOSED : 1
이제 OPEN 목록의 첫 번째 노드(예상 총 비용이 가장 낮은 노드)는 4가 된다.
노드 4는 노드 1,5,6에 연결되지만, 노드 1은 닫혀 있으므로 고려하지 않는다.
이때 노드 4에서 5로 간다고 하자.
현재 노드 5는 상위 노드가 노드 1이고, past cost가 30이다.(1->5)
그러나 노드 1->4->5에서의 경로 비용은 20에 불과하다.
이건 노드 4에 대한 past 비용에 4->5로 가는 8을 더한 값이다.
따라서 노드 5로 가는 새로운 최적 경로는 노드 4를 통과하며, past cost는 20이다.
그래서 노드 5의 정보를 업데이트한다.
그리고 이 변경 사항을 OPEN에 반영한다.
현재 OPEN : 4(22), 3(28), 5(30)
다음으로 노드 6의 정보를 업데이트하여 past cost를32(4의 past cost 12 + 간선의 cost 20)로 만들고,
optimist ctg는 원래 0이었으므로 32로 만든다.
현재 OPEN : 4(22), 3(28), 5(30),6(32)
| 5 | 6 | |
| past cost | 20 | 32 |
| optimist ctg | 10 | 0 |
| est total cost | 30 | 32 |
| parent node | 4 | 4 |
6에 도달했지만, 검색 과정은 끝나지 않는다.
앞으로도 노드 6으로 가는 더 저렴한 경로를 찾을 수 있다.
마찬가지로 4의 탐색이 완료되었으므로, closed로 이동시킨다.
현재 OPEN : 3(28), 5(30),6(32)
CLOSED : 1,4
다음으로 노드 3에서 탐색. 3->6은 15이고, 3->2는 27이다.
현재 3의 past cost는 18이므로, 3->2는 inf보다는 낫다. 그러므로 갱신해주면 55이고,
3->6은 18+15인데, 과거 비용보다 높다.
따라서 갱신하지 않는다.
| 2 | 6 | |
| past cost | 45 | 32 |
| optimist ctg | 10 | 0 |
| est total cost | 55 | 32 |
| parent node | 3 | 4 |
이제 또 다시 3을 CLOSED로 이동시킨다. OPEN에서는 2(55)가 추가
현재 OPEN : 5(30),6(32), 2(55)
이러한 수순으로 반복하면
5에 관해서는 당연히 20 10 30이므로, 20(past cost)+10 -> 6이 갱신. 그래서 6의 parent가 5가 된다.
현재 OPEN : 6(30), 2(55)
여기서 중요한 건, OPEN에 6(30)이 갱신되었는데
6은 당연히 goal이므로, 비용 추가 특성으로 인해, 이것보다 더 최적화된 값을 미래에 찾을 수는 없다.
그러므로 2까지도 가지 않고 search가 끝난다.
따라서 최종 최적화 값은 30이 된다.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| past cost | 0 | 45 | 18 | 12 | 20 | 30 |
| optimist ctg | 20 | 10 | 10 | 10 | 10 | 0 |
| est tot cost | 20 | 55 | 28 | 22 | 30 | 30 |
| parent node | - | 3 | 1 | 1 | 4 | 5 |
pseudo code는 다음과 같다.
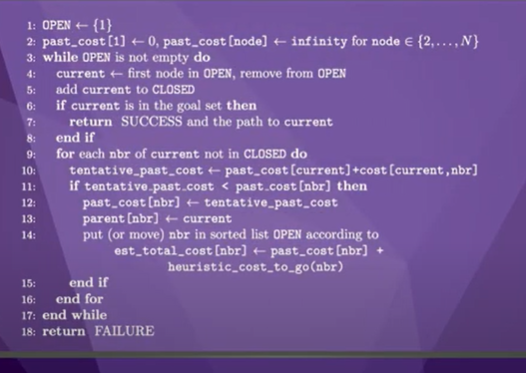
처음에 리스트를 만든다.
알고리즘을 초기화한 다음
while 루프에 들어가서, 탐색할 OPEN목록의 첫 번째 노드를 표시한다.
이 노드가 goal에 있다면 알고리즘은 최적의 솔루션을 찾는 데 성공한 것이며, 알고리즘을 종료합니다.
그렇지 않은 경우 알고리즘은 아직 CLOSED 되지 않은 각 그래프의 이웃을 탐색한다.
각 이웃 노드에 대해 알고리즘은 해당 노드에 대한 새로운 최적 경로를 찾았는지 확인하고,
그렇다면 노드의 과거 비용, 예상 총비용, 부모 노드, OPEN의 위치를 업데이트한다.
만약 OPEN 목록이 비어 있으면 모션 계획 문제에 대한 해결책이 없다.
이 알고리즘의 변형은 항상 Optimistic cost-to-go를 0으로 선택하는 것이다.
그러면 과거 비용과 예상 총 비용이 같다.
이 알고리즘이 바로 Dijkstra 알고리즘이다.
다익스트라도 최적의 경로를 찾지만, 검색을 안내하는 데 있어서 경험적 이동 비용을 사용하지 않기 때문에 일반적으로 A-star보다 훨씬 느리다.
따라서 가능하다면 Optimistic cost-to-go를 사용해야 한다.
