티스토리 뷰
D-H 매트릭스를 활용한 역기구학 구하기
Stanford Arm의 D-H 매트릭스 T
엔드 이펙터라고 하는 것을 별도의 프레임으로 구분한다.
7개의 매트릭스로 구성이 되는 T 매트릭스에서,
베이스 프레임 0~1의 inverser를 앞쪽에다가 곱해주고,
A의 5에서부터 6, 6에서부터 엔드 이펙터까지 가는 변환에 대한 인버스를 뒤에 곱해준다.

이렇게 제거해주는 이유는, 처음 베이스 포인트부터 끝점까지 가는 변환에 있어서 6개의 좌표계를 전부다 한번에 고려를 해서 구한다는 건 쉬운일이 아니다.
간단하게 접근하기 위해 이렇기 한다.
매니퓰레이터의 경우에는 대부분 사람의 손목에 해당하는 wrist joint가 존재한다.
이곳은 세개의 축이 교차하는 경우가 생긴다. 3개의 축의 원점이 같다.
그것을 활용하기 위해서 매트릭스를 만들어 준 것이다.
Position of W = F(세타1,세타2,세타3)만 있어도 표현할 수 있다
3~5는 같은 포지션에 있기 때문.

.
d-h 파라미터를 통해서, 5~6까지 오는 변환과 역변환을 먼저 구한다.
또 0~1의 역변한도 구한다.
주어진 T에다가 수식을 계산하면, W의 위치를 맨 뒤쪽의 값으로 구할 수 있다.


따라서, 최종적으로는 다음과 같은 식이 도출된다.

3개의 수식과 3개의 미지수를 바탕으로 어떻게 결정하는지를 살펴보자.

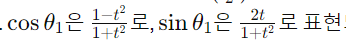
반각공식으로 정의한 것들을 바탕으로, (3)에 넣으면, 근의 공식이 되고,
그러므로 복수의 솔루션을 얻을 수 있다

이렇게 되면, 당연하게도 2*arctan로 감싸서, 세타1을 구할 수 있다.
(1)과 (2)는 (1) /(2)를 하면, 세타 2는

이렇게 되고, 마찬가지로 이 솔루션도 2개의 값으로 나온다.
그리고 (1)^2+(2)^2을 하면, d3도 구할 수 있다.

이제, 세타 1, 세타 2, d3는 구하게 되었다.
그러면 0~3까지의 d-h matrix는 알게 되었다.
그러면 다시 수식을 다음과 같이 정의할 수 있다.

T'를 구하기

새롭게 정의된 매트릭스를 프라임이라고 하자.
그러면, 34 inverse를 곱해주었을 때,

세타 4로만 이루어진 매트릭스가 하나 생긴다.
이렇게 주어지는 식의 앞에 곱해주면, 우변에는 이제 최종적으로 4~5,5~6변환만 남는다.
그 결과가 이렇게 된다.

이렇게 두 개의 변환 매트릭에서 3,3 eliment는 -ax's4+ay'c4=0이라는 수식이 주어진다.
이걸로 아크 탄젠트를 구하면, 세타4, 세타4+파이가 된다.
그 다음으로 1,3 / 2,3 element를 활용하면, 세타 5, -세타 5를 구할 수 있다.
마지막으로 3,1 / 3,2 element를 활용하면, 세타 6를 구할 수 있다.
역시 마찬가지로 탄젠트 값은 항상 복수의 값이 얻어지게 된다.
세타 6, 세타6+파이
만약 세타 4가 결정된다면, 그에 따라 세타5와 세타 6의 값도 달라진다.

만약에 세타5가 0이라면, 세타4+파이만 얻어질 수 있다.(degenerate)
5번째 축이 움직이지 않는 상태가 되면, 4번째,6번째 축은 같은 각도에서 회전하게 된다.
그렇기에 당연하게도 세타 6은 end-effector 입장에서는 같은 값을 반영하여 가동할 수 있는 범위가 결정된다.
전체적 이동 형상과 기능이 떨어지게 된다.
항상 발생할 수 있는 문제이므로, 항상 주의 깊게 살펴볼 필요가 있다.
